r5g.netlify.app

Abstract

• Bayesian Network Definition
• Dynamic Bayesian Networks Python

Motivation: Signaling pathways are dynamic events that take place over a given period of time. In order to identify these pathways, expression data over time are required. Dynamic Bayesian network (DBN) is an important approach for predicting the gene regulatory networks from time course expression data. However, two fundamental problems greatly reduce the effectiveness of current DBN methods. The first problem is the relatively low accuracy of prediction, and the second is the excessive computational time.

A Bayesian network, Bayes network, belief network, Bayes(ian). (Analogously, in the specific context of a dynamic Bayesian network. Notable software for Bayesian networks include: Just another Gibbs sampler (JAGS) - Open-source alternative to WinBUGS. Uses Gibbs sampling. DYNAMIC OPERATIONAL RISK ASSESSMENT WITH BAYESIAN NETWORK. Dynamic Operational Risk Assessment with Bayesian Network. (August 2012) Shubharthi Barua, B.Sc., Bangladesh University of Engineering & Technology. Dynamic Bayesian network with two time-slices. 60 Figure 18. Dry-out probability upon different equipment.

Results: In this paper, we present a DBN-based approach with increased accuracy and reduced computational time compared with existing DBN methods. Unlike previous methods, our approach limits potential regulators to those genes with either earlier or simultaneous expression changes (up- or down-regulation) in relation to their target genes. This allows us to limit the number of potential regulators and consequently reduce the search space. Furthermore, we use the time difference between the initial change in the expression of a given regulator gene and its potential target gene to estimate the transcriptional time lag between these two genes. This method of time lag estimation increases the accuracy of predicting gene regulatory networks. Our approach is evaluated using time-series expression data measured during the yeast cell cycle. The results demonstrate that this approach can predict regulatory networks with significantly improved accuracy and reduced computational time compared with existing DBN approaches.

Availability: The programs described in this paper can be obtained from the corresponding author upon request.

Contact:sconzen@medicine.bsd.uchicago.edu

INTRODUCTION

Genome-wide DNA microarrays are powerful tools, providing a glimpse of the signals and interactions within regulatory pathways of the cell. They enable the simultaneous measurement of mRNA abundance of most, if not all, identified genes in a genome under different physiological conditions. Because signaling pathways are dynamic events that take place over time, single time point expression profiles may not allow us to identify temporal events. This problem can be approached by performing a DNA microarray experiment with a series of time points following a physiological event.

Dynamic Bayesian network (DBN) analysis (Murphy and Mian, 1999; Imoto et al., 2002; Kim et al., 2003; Perrin et al., 2003) is well-suited for handling time-series gene expression data. To our knowledge, Murphy and Mian (1999) are to be credited with first employing DBN for modeling time-series expression data. In the DBN analysis, regulator–target gene pairs are usually identified based on a statistical analysis of their expression relationships across different time slices. For example, time slices T₁ for the regulator and T₂ for the target gene, where T₁ precedes T₂. The time period between the time slices of the regulator and target (T₂ − T₁) is considered as the transcriptional time lag. Specifically, it is the time that it takes for the regulator gene to express its protein product and the transcription of the target gene to be affected (directly or indirectly) by this regulator protein. Consequently, we are more likely to observe a significant statistical correlation between the expression of a regulator and its target if biologically relevant time slices are used.

There are two major problems with current DBN methods that greatly reduce their effectiveness. The first problem is the lack of a systematic way to determine a biologically relevant transcriptional time lag, which results in relatively low accuracy of predicting gene regulatory networks. The second problem is the excessive computational cost of these analyses, which limits the applicability of current DBN analyses to a large-scale microarray data. Therefore, this paper introduces a DBN-based analysis that can predict gene regulatory networks from time course expression data with significantly increased accuracy and reduced computational time. Our approach differs from existing DBN methods [typified by Murphy's Bayes Net Toolbox (BNT) at http://www.ai.mit.edu/~murphyk/Software/BNT/bnt.html] in two major ways. First, in BNT, all the genes in the dataset are considered as potential regulators of a given target gene. In contrast, our method focuses on employing the biological fact that most transcriptional regulators exhibit either an earlier or simultaneous change in the expression level when compared to their targets Yu et al., 2003. This limits the potential regulators of each target gene and thus significantly reduces the computational time. Second, in order to perform a statistical analysis of gene expression relationships, BNT generates a data matrix containing the time course expression profiles of the potential regulators and a given target gene. In this data matrix, the time course expression levels of all the potential regulators are aligned perfectly with each other throughout the time course. However, the expression levels of the target genes are misaligned with those of the potential regulators by one time unit. For example, the expression levels of the potential regulators at time point 1 are aligned with the expression level of the target gene at time point 2, where the time lag is just one time unit. Therefore, BNT automatically assumes that the time unit in a time course microarray experiment is the transcriptional time lag for all potential regulator–target pairs. This estimation of the transcriptional time lag can be inaccurate and results in a relatively low accuracy of predicting gene relationships using BNT. In contrast, our method proposes to use the time difference between the initial gene expression change of a potential regulator and its target as a reasonable estimation of the transcriptional time lag between these two genes, which can vary from zero (roughly simultaneous expression changes of the regulator and its target) to several time units. Based on these improvements, we expect that our DBN approach will uncover gene–gene relationships with a significantly increased accuracy and reduced computational time compared with existing DBN methods. The final steps in both our method and BNT are to calculate the conditional probabilities of the target gene expression in relation to the expression of its potential regulators, and subsequently the ‘log marginal likelihood score’. Potential regulator(s) with the highest log marginal likelihood score will be ultimately selected as the final set of regulators for the given target gene. A conceptual representation of our approach is presented in Figure 1, and a detailed description of our method is presented in the Methods section.

MATERIALS: DATA AND SOFTWARE

To evaluate our approach, we report the analysis of the yeast cell cycle time-series gene expression data from Chou et al. (1998). This dataset has a large number of time points (n = 16) with relatively small time intervals (10 min), thus making it ideal for testing our approach. In addition, the yeast cell cycle has many previously established gene regulatory relationships (Simon et al., 2001), allowing ready confirmation of the accuracy of our algorithm-derived gene–gene relationships. For example, the Chou et al. (1998) yeast dataset contains 116 known cell cycle genes that encode either transcription factors (TFs) or their established targets. These genes can be inputted into our algorithm and predicted relationships are then verified by the comparison with established relationships.

Since Murphy's BNT already provides the necessary functionalities for building Bayesian networks, we implemented our new DBN analysis within the framework of BNT. The details of our approach are described in the ‘Methods’ section. The supporting programs to initially determine up- or down-regulation of individual genes and the transcriptional time lags between potential regulators and their targets are written in Java. These programs can be obtained from the corresponding author upon request.

Tuneup Utilities 2018 key with Crack Full Version [New] Tuneup Utilities 2018 Crack is very useful setup for your system. It requires maintenance and tuning more often than one would believe it does. This is why the. More popularly known as the one-click solution for users in the tech world. If this application is present on your system. 1-Click M3U Maker is one of the quickest and easiest to use tools of its kind.1 Click Maintenance Free Download Full Version.. Tuneup 1 click maintenance free full version.. Of the most useful Windows-related tools in one free download.Weve upgraded TuneUp Utilities to give you longer battery life and more disk space on your Windows PC. With our 2014 version. AVG PC TuneUp TuneUp Utilities 15.0.1001.393 License Trial version Language English Platform windows. Optimize PC performance, fix problems and customize your system. Tune Up Utilities 2010 1 click maintenance. Tune Up Utilities 2010 1 click maintenance is hosted at free file sharing service. Share Add to my account. Tuneup 1 click maintenance full version. AVG PC TuneUp Utilities 2019 Full Torrent is famous as the one-click solution for users in the entire world that used advanced technology. Our suggestions that are a real range of tools let you fine tune for even more performance. With AVG PC TuneUp Utilities 2019 Keygen Latest Version, you can also install AVG Cleaner PRO on.

METHODS

In this section, we describe the details of our DBN approach using the analysis of a set of hypothetical expression data as an example. This example includes four hypothetical genes A–D and their expression data at six evenly spaced time points T₁–T₆.

Step 1: Selection of potential regulators for each gene

We first determined the time points of the initial changes in the expression (up- or down-regulation) of genes A–D based up on their time-series expression data. Although there is currently no gold standard for determining what this threshold is for up- or down-regulation, we decided to use ≥1.2-fold (up-regulation) and ≤0.70-fold (down-regulation) compared to baseline gene expression as the cutoffs. Although these are relatively modest cutoffs, we did not want to miss genes with small, but potentially important changes in gene expression. We then determined the time points of the initial up- or down-regulation of genes A–D, and assigned genes with earlier or simultaneous changes in expression as the potential regulators of those genes with a later change in expression. In this way, we were able to select a subset of potential regulator genes for any given target gene.

The results of this potential regulator pre-selection for genes A–D are shown in Figure 2. Based on the criteria above for determining up- or down-regulated expression, the initial up-regulation of genes A and B occurs at T₂, gene C is initially up-regulated at T₃, and gene D is initially up-regulated at T₄. We selected genes A–C as the potential regulators of gene D because the initial up-regulation of genes A–C precedes that of gene D. This is followed by similar selection of potential regulators for other genes. In Figure 2, we illustrate a case of up-regulated expression, but similar potential regulator selection applies to down-regulated genes as well.

Step 2: Estimation of biologically relevant transcriptional time lag

After potential regulator selection, we next performed an estimation of the transcriptional time lag between potential regulators and their target genes. We propose that the time difference between the initial expression change of a potential regulator and its target gene represents a biologically relevant time period. This is expected to allow a more accurate estimation of the transcriptional time lag between potential regulators and their targets, because it takes into account variable expression relationships of different regulator–target pairs.

As an example, we illustrate the estimated time lags between target gene D and its potential regulators in Figure 3. We estimated that the time lags between potential regulators of genes A–C and their potential target gene D are two time units, two time units and one time unit, respectively. We then performed similar predictions for other potential regulator–target pairs. Of note, the transcriptional time lag estimated by our method can vary from zero to several time units. Since each target gene can have more than one regulator, we divided the potential regulators of each gene into different groups based on the individual transcriptional time lag with the target gene. As an example, we put genes A and B into one group since they have the same transcriptional time lag of two time units with respect to target gene D; gene C was placed in another group because it has a time lag of only one time unit with respect to gene D. The rationale for separating potential regulators into different groups is that different regulators may regulate the same target gene in either different time frames or in the same time frame. This allows us to analyze different potential regulators separately while grouping potential co-regulators together.

Step 3: Gene regulatory network modeling

The variables in our DBN analysis are the gene expression levels across different time points in the time course expression data. However, we did not use the absolute fold-change values, instead, we assigned ‘2’ if the expression level is equal to or higher than the average expression level for that gene across all time points, and ‘1’ if the expression level is lower than the average level. Note that we did not use the ≥1.2- or ≤0.70-fold cutoffs (see Step 1) to assign absolute up- or down-regulation to the expression level at each time point, instead we focused on the relative increase or decrease in expression levels. This is because the main focus of DBN is to identify the correlation between gene expression patterns, rather then their absolute expression value at any one particular time point.

We then used the results from Steps 1 and 2 to more accurately predict gene regulatory networks from time-series expression data, which are demonstrated by using the same example as in Steps 1 and 2. As stated in Step 2, we divided potential regulators of gene D into two groups based on their transcriptional time lags with gene D: a group of genes A and B with two time units as the transcriptional time lag with gene D, and gene C with one time unit as the time lag with gene D. For each group of potential regulators, we then generated all the subsets of this group, based on the user's pre-defined minimum and maximum number of regulators. This is because the number of co-regulators of a given target gene is unknown. The generation of the subsets of each group of potential regulators allows us to examine the expression relationships between all possible sets of co-regulators and their target gene. Therefore, the subsets of genes A and B are {gene A}, {gene B} and {gene A, gene B}; the subset of gene C is itself: {gene C}. Then, for each subset of potential regulators, we used the transcriptional time lag estimated in Step 2 to organize the expression data of the potential regulators and their target gene into an N × M matrix, where N is the number of the potential regulators plus the target gene, T is the number of time points in the original time series expression data, t is the estimated transcriptional time lag (represented by the number of time units) and M is the number of time points in the data matrix which is equal to T − t. Therefore, in this matrix, the expression value of the potential regulators at time T₁ are aligned with the expression value of the target gene at time T₁ + t, where t is the estimated transcriptional time lag. Note that the t-value (transcriptional time lag in time point units) may vary in different expression data matrices. In Figure 4A, we illustrate the data matrix for subset gene A with its target gene D.

After constructing expression data matrices of all target genes with their potential regulators, we calculated the conditional probabilities of each target gene in relation to its regulator genes based on the data matrices. The conditional probabilities of the expression of gene D in relation to the expression of gene A are shown in Figure 4B. Marginal likelihood scores were then calculated using these conditional probabilities. For each target gene, we then selected the subset of potential regulator(s) that gives the highest log marginal likelihood score as the final set of regulators for this target gene.

RESULTS

In DBN analyses of time-series expression data, at least two situations can exist. First, one might have some prior knowledge of the system studied, such as the identity of TFs in the system even though the targets of the TFs are unknown. Indeed, if we know the identity of the TFs in the system, we can use this prior knowledge to limit the potential regulators of each gene in the dataset to only these TFs, and then identify the targets of these TFs. In the second situation, we may not have any prior knowledge of the system, and thus need to identify regulatory networks by considering all potential regulator–target pairs. Therefore, in this work, we performed two sets of experiments to represent both of these possibilities.

In each experiment, we used both our approach and Murphy's BNT to analyze Chou et al.'s yeast cell cycle data, and compared the accuracy and the computational cost of the two methods. In Experiment 1, we only allowed the nine TFs to be the possible regulators of the 116 genes in the dataset (including the nine TFs, because a given TF can be regulated by other TFs), and we identified the targets of these nine TFs. We denote the learned networks using our method and BNT as DBN_{our_1} and DBN_{BNT_1}, respectively. In Experiment 2, we excluded any prior knowledge of the yeast cell cycle, thus allowing all potential regulator–target pairs and subsequently identified the relationships between these 116 genes solely based on the time course microarray data. Regulatory networks identified using our method versus BNT in Experiment 2 are listed as DBN_{our_2} and DBN_{BNT_2}.

The results of Experiment 1 are summarized in Table 1, and the results of Experiment 2 are listed in Table 2. In both tables, row (I) represents the network identified by our method, and row (II) represents the network learned using BNT. ‘Correctly identified relationships’ specifies predicted relationships that have been established in yeast cell cycle regulation. ‘Misdirected relationship’ represents a gene relationship that is predicted to be in the reverse order of a known relationship. ‘Specificity’ is the percentage of correctly predicted known gene relationships out of the total number of predicted gene relationships. ‘Computational time’ is the running time of the analysis.

Experiment 1

Since we only allow the nine TFs to be the potential regulators in Experiment 1, the search space is relatively small and thus the computational time for both methods is relatively short. However, a close comparison of the computational times demonstrates a completion time of 10 s for our method and 60 s for Murphy's method (Table 1). The difference between the computational times is much more dramatic when the number of potential regulators increases as in Experiment 2.

In DBN_{our_1}, by selecting potential regulators based on their concurrent or antecedent change in expression in relation to the target genes, the number of misdirected relationships decreases from four (DBN_{BNT_1}) to one (DBN_{our_1}) (Table 1). Interestingly, the four misdirected relationships in DBN_{BNT_1} were all correctly reversed in DBN_{our_1}. Examination of the expression profiles of these four misdirected relationships reveals an earlier expression change of the known regulator gene compared with the target gene. For example, SWI4, a TF, is known to regulate gene NDD1Simon et al., 2001. However, SWI4 was erroneously determined to be the target of NDD1 in DBN_{BNT_1}. Interestingly, using our method, SWI4 becomes a regulator of NDD1. SWI4's expression is up-regulated for 10 min compared with NDD1's up-regulation for 20 min. However, NDD1 apparently has a strong statistical relationship with SWI4 based on their expression data, which results in the regulation of SWI4 by NDD1 in DBN_{BNT_1}. In our method, NDD1 is excluded from being a potential regulator of SWI4 because it has a delayed expression change compared with SWI4, and thus is not likely to be a regulator of SWI4. This results in assigning SWI4 as a potential regulator of NDD1, and our statistical analysis confirmed that SWI4 is a regulator of NDD1. Therefore, the misdirected relationship NDD1 → SWI4 in DBN_{BNT_1} was correctly reversed to SWI4 → NDD1 in DBN_{our_1}.

Interestingly, there is only one misdirected relationship in DBN_{our_1}. In this relationship, SWI5, although known to be a transcriptional target of NDD1Simon et al., 2001, is predicted by our method to be a regulator of NDD1 (SWI5 → NDD1). This misdirected relationship is caused by the antecedent up-regulation of SWI5 for 10 min compared with NDD1's up-regulation for 20 min. Therefore, SWI5 was selected by our method to be the regulator of NDD1, instead of vice versa. A further statistical analysis also confirmed the regulation directed from SWI5 to NDD1. This finding indicates that even though most transcriptional regulators have either an earlier or simultaneous change in expression compared with their targets, there are exceptions. Earlier expression change of the target gene in comparison with that of the regulator gene may be caused by the different mRNA half-lives of the regulator gene and target gene, and may also suggest a feedback loop, where a target gene can in turn regulates its regulator. However, a further examination of Chou et al.'s yeast cell cycle time-series data showed that in 70% of the known yeast gene–gene relationships, the regulator gene has either an earlier or simultaneous expression change compared with its target gene. This suggests the general applicability of our method in discovering gene regulatory relationships.

The results from our analysis of yeast cell cycle expression data demonstrate that our method is capable of identifying a higher number of known gene–gene relationships compared with BNT. The number of correctly identified, already established gene–gene relationships increased significantly from 18 in DBN_{BNT_1} to 46 in DBN_{our_1} (Table 1). A close examination of the 36 gene–gene relationships correctly identified by our method (Table 3) and not by BNT reveals that all 36 relationships have a much stronger statistical correlation using the estimated transcriptional time lags compared with using the single time unit (10 min) as the time lag. As an example, SWI4, a TF, is known to transcriptionally regulate MBP1Simon et al., 2001. However, this relationship was rejected by BNT because there is no significant statistical correlation between SWI4 and MBP1 expression when using a single time unit as the transcriptional time lag for the statistical analysis. This is illustrated by the low conditional probability of MBP1's expression correlating with SWI4's expression using the 10 minute time lag (Fig. 5A). However, when using a 30 min time difference (three time units) between the initial expression change of SWI4 and MBP1, a strong statistical correlation was uncovered (Fig. 5B).

In contrast to the 36 known gene–gene relationships identified by our method exclusively, there are only eight relationships that are identified exclusively by BNT (Table 3). Three of these eight relationships have a better correlation if using 10 min as the transcriptional time lag compared with using the zero minute time lag estimated by our analysis. The other five relationships resulted from earlier expression changes of the target gene compared with their regulators.

Experiment 2

In this experiment, we compared the accuracy and efficiency of our method with BNT when no prior knowledge of yeast cell cycle TFs was inputted into the DBN model. This experiment allowed all the genes being analyzed to be potential regulators rather than only the nine TFs as in Experiment 1.

The difference between the computational cost of our method and BNT is even more dramatic in this experiment than in Experiment 1. The completion time for running our analysis on the dataset of 116 genes was only 15 min, while it took 8 h using BNT (Table 2).

As in Experiment 1, the number of misdirected relationships drops significantly from seven in DBN_{BNT_2} to three in DBN_{our_2} (Table 2). One misdirected relationship occurs in both networks. A close examination of the other six misdirected relationships in DBN_{BNT_2} reveals that these relationships include known regulators, which have an earlier initial expression change than their targets. Since the statistical analysis is the only measure to determine regulator–target pairs in BNT, the apparent statistical correlation erroneously determined the regulation from the known target gene to the known regulator gene in these six misdirected relationships. Interestingly, five of these six misdirected relationships were successfully reversed in our analysis. The other misdirected relationship was not reversed in our analysis due to an insignificant statistical correlation between the genes in this known relationship. Compared with the seven misdirected relationships in DBN_{BNT_2}, there are only three in DBN_{our_2}. The three misdirected relationships were caused by the fact that the known regulator has a later change in expression than its known target.

Not everyone will have used iFile, but it’s fair to suggest that a fairly high percentage of device owners will have at least heard of it. How to download ifile without jailbreak or openappmkt. IFile is an app which is likely going to be familiar to most.

The advantage of using a more biologically relevant estimation of the transcriptional time lag is clearly reflected in these results. Twelve established relationships were correctly identified by our approach and not by BNT. Out of these 12 relationships, 10 have estimated transcriptional time lags other than 10 min, which is the arbitrary time lag used in BNT. In addition, all of the 10 relationships have much stronger statistical correlations when using their transcriptional time lags estimated in our method compared with using the 10 min time lag. Compared with the 12 known relationships identified in DBN_{our_2} (and not in DBN_{BNT_2}), there are only three that are identified exclusively in DBN_{BNT_2}. Two of the three relationships were not identified by our method because the known regulators in these relationships have later changes in expression than their targets. The other relationship was not identified by our method because it has a better statistical correlation if using a 10 min time lag compared with using the 20 min time lag we estimated in our analysis.

From the results of both experiments, we can see that the number of correctly identified known relationships decreases in Experiment 2 when compared with Experiment 1. This finding reflects the fact that when we increase the number of potential regulators, the number of possible false positive predictions increases. However, if we reduce the number of potential regulators, we might miss uncovering interesting regulator–target pairs. This dilemma may be solved when we possess a more thorough understanding of the transcriptional regulation.

CONCLUSIONS

In this paper, we address two fundamental problems associated with current DBN analyses: (1) a low accuracy of predicted gene–gene relationships attributed to the arbitrary assignment of a transcriptional time lag and (2) an extremely long computational time due to the lack of an efficient approach to reduce the search space. In our approach, we consider the fact that gene regulators usually have either a simultaneous or antecedent changes in expression when compared to their targets. This consideration allows us to limit possible regulators of each gene thus reducing the search space. Furthermore, we use the time difference between the initial change in expression of a given regulator gene and its potential target gene to estimate the transcriptional time lag between these two genes. This estimation of transcriptional time lag increases the accuracy of predicting gene regulatory networks. In our current analysis, we used established TF–target relationships as measured by a genome-wide screen of promoter binding by tagged TFs to define correct gene–gene interactions Simon et al., 2001. Additional large-scale promoter binding screens have also been performed Horak et al., 2002 and are complementary approaches to a DBN-based analysis of global gene expression. Although assessment of the absolute predictive accuracy of any DBN method is limited by our current knowledge of established gene–gene interactions, our new method appears to be more accurate than traditional BNT in predicting gene–gene relationships.

In our analysis, we estimated the transcriptional time lag between a regulator gene and a target gene as the time difference between their initial expression change. The time points of the initial expression change (up- or down-regulation) of a gene could be affected by the cutoffs we use to determine the significantly up- or down-regulated expression. Therefore, there can be error associated with the transcriptional time lag estimated by our method. Further work on how to most accurately determine thresholds of significant up- or down-regulation needs to be conducted.

Another important consideration is the noise in microarray gene expression data. One approach to deal with uncertainty in expression data is to perform replicate experiments of the same time course microarray experiment. Experiments can then be analyzed in at least two different ways. The first approach is to consider each dataset separately, which will result in independent gene regulatory networks for each dataset. We could then identify gene relationships that occur in the majority of the independently predicted networks. This approach may filter out false gene relationships that are caused by random noise, and therefore are not likely to occur consistently in different experiments. The second approach is to average the expression levels of each gene from independent replicates, and assign a standard error (SE) to each averaged value. We can then perform similar DBN analysis on this averaged data as described in the ‘Methods’ section. We could then use a scoring function that takes the standard errors into account instead of the ‘log marginal likelihood’ score that assumes the certainty of the expression values. We could redesign the scoring function so that gene relationships that have small standard errors for the averaged expression of its regulator genes and target genes will have a higher score, and will be given more weight than those gene relationships with higher standard errors. However, the first approach may be a better choice, because averaging may cause the loss of a significant relationship if the expression values of one experiment are particularly noisy.

Finally, we have shown that occasionally the expression of a target gene precedes that of the regulator gene. While this is an uncommon phenomenon, especially in eukaryotic cells, the occurrence of this phenomenon may be caused by several factors. The first factor is the variability of mRNA half-lives. For example, if the regulator gene's encoded mRNA has a significantly shorter half-life than that of its target gene, it may take the regulator's mRNA much longer to reach a significantly up- or down-regulated steady-state level when compared with the time it takes for the target's mRNA to undergo a significant change in steady-state expression level. This could lead to an apparently earlier time of threshold expression change of the target gene compared to its regulator gene. Taking variable mRNA half-lives into account is a current challenge for DBN developers. The second factor is the existence of gene regulatory feedback loops. The fact that a known target gene's change in expression occurs earlier than that of its known regulator gene may suggest a feedback loop, where the target gene can also regulate the regulator gene. However, a further examination of Chou et al.'s yeast cell cycle time-series data showed that in 70% of the known yeast gene–gene relationships, the regulator gene has either an earlier or simultaneous expression change compared with its target gene. This suggests a general applicability of our method in discovering gene regulatory relationships and providing testable hypotheses. Because many biological signaling networks involve key transcriptional events, this approach may be used to predict hypothetical gene regulatory networks from time course microarray data. For example, the transcriptional changes that follow growth factor or nuclear hormone receptor activation will lend themselves to this type of analysis.

A conceptual view of our DBN-based approach. 1, Identification of the time point of the initial expression change (up- or down-regulation) of each gene based on the microarray time course expression data. 2, Potential regulators are limited to those with simultaneous or antecedent expression changes when compared with their target genes (R, potential regulation). 3, Estimation of the transcriptional time lag between the potential regulator and its target gene as the time difference between initial expression changes of these two genes. 4, DBN: statistical analysis of the expression relationship between the potential regulator and its target gene in time slices that represent the transcriptional time lag between these two genes (as estimated in 3). 5, Predicted gene regulatory network.

A conceptual view of our DBN-based approach. 1, Identification of the time point of the initial expression change (up- or down-regulation) of each gene based on the microarray time course expression data. 2, Potential regulators are limited to those with simultaneous or antecedent expression changes when compared with their target genes (R, potential regulation). 3, Estimation of the transcriptional time lag between the potential regulator and its target gene as the time difference between initial expression changes of these two genes. 4, DBN: statistical analysis of the expression relationship between the potential regulator and its target gene in time slices that represent the transcriptional time lag between these two genes (as estimated in 3). 5, Predicted gene regulatory network.

Step 1: the dynamic expression profiles of genes A–D and the time points of their initial up-regulated expressions. Potential regulators are selected based on their simultaneous or antecedent expression change when compared with the expression change of their respective target gene.

Step 1: the dynamic expression profiles of genes A–D and the time points of their initial up-regulated expressions. Potential regulators are selected based on their simultaneous or antecedent expression change when compared with the expression change of their respective target gene.

Step 2: the transcriptional time lag between the potential regulator and its target gene is estimated as the time difference between the initial expression change of these two genes.

Step 2: the transcriptional time lag between the potential regulator and its target gene is estimated as the time difference between the initial expression change of these two genes.

Step 3: (A) Discrete expression values of potential regulator gene A and its target gene D are placed in a data matrix, where the expression level of gene A at time point T is aligned with the expression level of gene D at time point T + t (t is the transcriptional time lag between genes A and D as estimated in Step 2). (B) The conditional probabilities of the expression of target gene D in relation to its potential regulator gene A are then calculated based on this data matrix.

Step 3: (A) Discrete expression values of potential regulator gene A and its target gene D are placed in a data matrix, where the expression level of gene A at time point T is aligned with the expression level of gene D at time point T + t (t is the transcriptional time lag between genes A and D as estimated in Step 2). (B) The conditional probabilities of the expression of target gene D in relation to its potential regulator gene A are then calculated based on this data matrix.

The results of Experiment 1 (incorporating prior knowledge of TFs)

(A) DBN_{our_1}

SWI4	PCL1	SWI4	NDD1	FKH1	SWI6
SWI4	CLN2	FKH1	ACE2	SWI4	MBP1
SWI4	OCH1	NDD1	ACE2	SWI4	PCL2
SWI4	HO	SWI6	SIM1	SWI4	CLB6
MCM1	STE6	SWI4	FKS1	MCM1	SIM1
MCM1	PIR3	FKH2	GIC1	FKH2	CLB4
SWI4	SWE1	SWI4	SPT21	SWI6	CDC6
SWI4	GIN4	SWI4	RSR1	SWI6	AGA1
FKH1	BUD8	SWI4	CWP1	MCM1	MFA1
ACE2	SPO12	MCM1	CLN3	SWI5	MFA2
MCM1	CLN2	FKH1	UTR2	SWI4	CLB2
SWI4	RNR1	MCM1	GIN4	SWI4	PLB3
FKH1	HHF_1	SWI4	YBR071W	SWI5	YLR463
SWI6	HTB2	SWI6	YPR075	SWI6	SPO12
SWI5	EGT2	NDD1	CDC20
SWI4	MNN1	SWI4	BUD4
(B) DBNBNT_1
SWI4	PCL1	ACE2	SPO12	MBP1	CLB6
SWI4	CLN2	SWI4	GIN4	SWI4	HTA2
SWI4	HO	FKH1	BUD8	SWI6	RSR1
SWI4	OCH1	MCM1	PIR3	FKH2	ACE2
MCM1	STE6	SWI4	BUD9	FKH1	SWI5
SWI4	SWE1	SWI6	CIS3	SWI5	HSP150

(A) DBN_{our_1}

SWI4	PCL1	SWI4	NDD1	FKH1	SWI6
SWI4	CLN2	FKH1	ACE2	SWI4	MBP1
SWI4	OCH1	NDD1	ACE2	SWI4	PCL2
SWI4	HO	SWI6	SIM1	SWI4	CLB6
MCM1	STE6	SWI4	FKS1	MCM1	SIM1
MCM1	PIR3	FKH2	GIC1	FKH2	CLB4
SWI4	SWE1	SWI4	SPT21	SWI6	CDC6
SWI4	GIN4	SWI4	RSR1	SWI6	AGA1
FKH1	BUD8	SWI4	CWP1	MCM1	MFA1
ACE2	SPO12	MCM1	CLN3	SWI5	MFA2
MCM1	CLN2	FKH1	UTR2	SWI4	CLB2
SWI4	RNR1	MCM1	GIN4	SWI4	PLB3
FKH1	HHF_1	SWI4	YBR071W	SWI5	YLR463
SWI6	HTB2	SWI6	YPR075	SWI6	SPO12
SWI5	EGT2	NDD1	CDC20
SWI4	MNN1	SWI4	BUD4
(B) DBNBNT_1
SWI4	PCL1	ACE2	SPO12	MBP1	CLB6
SWI4	CLN2	SWI4	GIN4	SWI4	HTA2
SWI4	HO	FKH1	BUD8	SWI6	RSR1
SWI4	OCH1	MCM1	PIR3	FKH2	ACE2
MCM1	STE6	SWI4	BUD9	FKH1	SWI5
SWI4	SWE1	SWI6	CIS3	SWI5	HSP150

(A) By our method. (B) By BNT. Relationships in italicized bold face type were identified by both our method and BNT. Relationships in normal font were identified by the corresponding method and not be the other method.

Correctly identified known gene–gene relationships in Experiment 1

(A) DBN_{our_1}

SWI4	PCL1	SWI4	NDD1	FKH1	SWI6
SWI4	CLN2	FKH1	ACE2	SWI4	MBP1
SWI4	OCH1	NDD1	ACE2	SWI4	PCL2
SWI4	HO	SWI6	SIM1	SWI4	CLB6
MCM1	STE6	SWI4	FKS1	MCM1	SIM1
MCM1	PIR3	FKH2	GIC1	FKH2	CLB4
SWI4	SWE1	SWI4	SPT21	SWI6	CDC6
SWI4	GIN4	SWI4	RSR1	SWI6	AGA1
FKH1	BUD8	SWI4	CWP1	MCM1	MFA1
ACE2	SPO12	MCM1	CLN3	SWI5	MFA2
MCM1	CLN2	FKH1	UTR2	SWI4	CLB2
SWI4	RNR1	MCM1	GIN4	SWI4	PLB3
FKH1	HHF_1	SWI4	YBR071W	SWI5	YLR463
SWI6	HTB2	SWI6	YPR075	SWI6	SPO12
SWI5	EGT2	NDD1	CDC20
SWI4	MNN1	SWI4	BUD4
(B) DBNBNT_1
SWI4	PCL1	ACE2	SPO12	MBP1	CLB6
SWI4	CLN2	SWI4	GIN4	SWI4	HTA2
SWI4	HO	FKH1	BUD8	SWI6	RSR1
SWI4	OCH1	MCM1	PIR3	FKH2	ACE2
MCM1	STE6	SWI4	BUD9	FKH1	SWI5
SWI4	SWE1	SWI6	CIS3	SWI5	HSP150

(A) DBN_{our_1}

SWI4	PCL1	SWI4	NDD1	FKH1	SWI6
SWI4	CLN2	FKH1	ACE2	SWI4	MBP1
SWI4	OCH1	NDD1	ACE2	SWI4	PCL2
SWI4	HO	SWI6	SIM1	SWI4	CLB6
MCM1	STE6	SWI4	FKS1	MCM1	SIM1
MCM1	PIR3	FKH2	GIC1	FKH2	CLB4
SWI4	SWE1	SWI4	SPT21	SWI6	CDC6
SWI4	GIN4	SWI4	RSR1	SWI6	AGA1
FKH1	BUD8	SWI4	CWP1	MCM1	MFA1
ACE2	SPO12	MCM1	CLN3	SWI5	MFA2
MCM1	CLN2	FKH1	UTR2	SWI4	CLB2
SWI4	RNR1	MCM1	GIN4	SWI4	PLB3
FKH1	HHF_1	SWI4	YBR071W	SWI5	YLR463
SWI6	HTB2	SWI6	YPR075	SWI6	SPO12
SWI5	EGT2	NDD1	CDC20
SWI4	MNN1	SWI4	BUD4
(B) DBNBNT_1
SWI4	PCL1	ACE2	SPO12	MBP1	CLB6
SWI4	CLN2	SWI4	GIN4	SWI4	HTA2
SWI4	HO	FKH1	BUD8	SWI6	RSR1
SWI4	OCH1	MCM1	PIR3	FKH2	ACE2
MCM1	STE6	SWI4	BUD9	FKH1	SWI5
SWI4	SWE1	SWI6	CIS3	SWI5	HSP150

(A) By our method. (B) By BNT. Relationships in italicized bold face type were identified by both our method and BNT. Relationships in normal font were identified by the corresponding method and not be the other method.

We thank Dr Dan Nicolae and Dr William Hsu for their constructive suggestions regarding the development of our DBN approach. This work was supported by NIH grants CA90459, CA89208, ES0123282 and the Entertainment Industry Foundation.

REFERENCES

Chou, R.J., Campbell, M.J., Winzeler, E.A., Steinmetz,L., Conway,A., Wodicka, L., Wolfsberg, T.G., Gabrielian, A.E., Landsman, D., Lockhart, D.J., Davis, R.W. A genome-wide transcriptional analysis of the mitotic cell cycle. –73Horak, C.E., Luscombe, N.M., Qian, J., Bertone, P., Spiccirrillo, S., Gerstein, M., Snyder, M. Complex transcriptional circuitry at the G₁/S transition in Saccharomyces cerevisiae . –3033Imoto, S., Goto, T., Miyano, S. Estimation of genetic networks and functional structures between genes by using Bayesian network and nonparametric regression. –186Kim, S.Y., Imoto, S., Miyano, S. Inferring gene networks from time series microarray data using dynamic Bayesian networks. –235Murphy, K. and Mian, S. Modeling gene expression data using dynamic Bayesian networks. , Berkeley, CA Computer Science Division, University of CaliforniaPerrin, B.E., Ralaivola, L., Mazurie, A., Bottani, S., Mallet, J., D'Alche-Buc, F. Gene networks inference using dynamic Bayesian networks. (Suppl.2), pp. –II148Simon, I., Barnett, J., Hannett, N., Harbison, C.T., Rinaldi, N.J., Volkert, T.L., Wyrick, J.J., Zeitlinger, J., Gifford, D.K., Jaakkola, T.S., Young, R.A. Serial regulation of transcriptional regulators in the yeast cell cycle. –708Yu, H., Luscombe, N.M., Qian, J., Gerstein, M. Genomic analysis of gene expression relationships in transcriptional regulatory networks. –427

Part of a series on Statistics
Bayesian statistics
Theory
Techniques

A Bayesian network, Bayes network, belief network, decision network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (e.g.speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.

• 3Inference and learning
• 4Statistical introduction
• 5Definitions and concepts
  • 5.4Markov blanket

Graphical model[edit]

Formally, Bayesian networks are DAGs whose nodes represent variables in the Bayesian sense: they may be observable quantities, latent variables, unknown parameters or hypotheses. Edges represent conditional dependencies; nodes that are not connected (no path connects one node to another) represent variables that are conditionally independent of each other. Each node is associated with a probability function that takes, as input, a particular set of values for the node's parent variables, and gives (as output) the probability (or probability distribution, if applicable) of the variable represented by the node. For example, if ${\displaystyle m}$ parent nodes represent ${\displaystyle m}$Boolean variables then the probability function could be represented by a table of ${\displaystyle 2^m}$ entries, one entry for each of the ${\displaystyle 2^m}$ possible parent combinations. Similar ideas may be applied to undirected, and possibly cyclic, graphs such as Markov networks.

Example[edit]

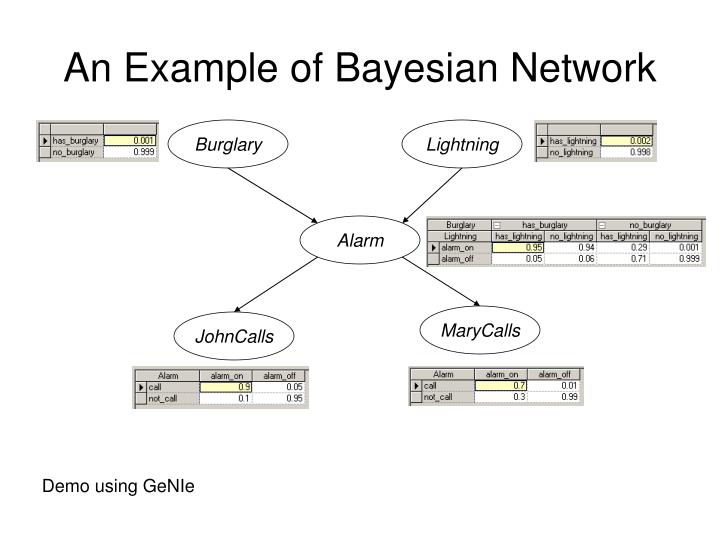
Two events can cause grass to be wet: an active sprinkler or rain. Rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler usually is not active). This situation can be modeled with a Bayesian network (shown to the right). Each variable has two possible values, T (for true) and F (for false).

The joint probability function is:

${\displaystyle Pr(G,S,R)=Pr(GS,R)Pr(SR)Pr(R)}$

where G = Grass wet (true/false), S = Sprinkler turned on (true/false), and R = Raining (true/false).

The model can answer questions about the presence of a cause given the presence of an effect (so-called inverse probability) like 'What is the probability that it is raining, given the grass is wet?' by using the conditional probability formula and summing over all nuisance variables:

${\displaystyle Pr(R=TG=T)=\frac{Pr(G=T,R=T)}{Pr(G=T)}=\frac{\sum _{S\in \{T,F\}}Pr(G=T,S,R=T)}{\sum _{S,R\in \{T,F\}}Pr(G=T,S,R)}}$

Using the expansion for the joint probability function ${\displaystyle Pr(G,S,R)}$ and the conditional probabilities from the conditional probability tables (CPTs) stated in the diagram, one can evaluate each term in the sums in the numerator and denominator. For example,

Then the numerical results (subscripted by the associated variable values) are

${\displaystyle Pr(R=TG=T)=\frac{{0.00198}_{TTT}+{0.1584}_{TFT}}{{0.00198}_{TTT}+{0.288}_{TTF}+{0.1584}_{TFT}+{0.0}_{TFF}}=\frac{891}{2491}\approx 35.77\mathrm{\%}.}$

To answer an interventional question, such as 'What is the probability that it would rain, given that we wet the grass?' the answer is governed by the post-intervention joint distribution function

${\displaystyle Pr(S,R\text{do}(G=T))=Pr(SR)P(R)}$

obtained by removing the factor ${\displaystyle Pr(GS,R)}$ from the pre-intervention distribution. The do operator forces the value of G to be true. The probability of rain is unaffected by the action:

${\displaystyle Pr(R\text{do}(G=T))=Pr(R)}$.

To predict the impact of turning the sprinkler on:

${\displaystyle Pr(R,G\text{do}(S=T))=Pr(R)Pr(GR,S=T)}$

with the term ${\displaystyle Pr(S=TR)}$ removed, showing that the action affects the grass but not the rain.These predictions may not be feasible given unobserved variables, as in most policy evaluation problems. The effect of the action ${\displaystyle \text{do}(x)}$ can still be predicted, however, whenever the back-door criterion is satisfied.^[1][2] It states that, if a set Z of nodes can be observed that d-separates^[3] (or blocks) all back-door paths from X to Y then

${\displaystyle Pr(Y,Z\text{do}(x))=Pr(Y,Z,X=x)/Pr(X=xZ)}$.

A back-door path is one that ends with an arrow into X. Sets that satisfy the back-door criterion are called 'sufficient' or 'admissible.' For example, the set Z = R is admissible for predicting the effect of S = T on G, because Rd-separates the (only) back-door path S ← R → G. However, if S is not observed, no other set d-separates this path and the effect of turning the sprinkler on (S = T) on the grass (G) cannot be predicted from passive observations. In that case P(G do(S = T)) is not 'identified'. This reflects the fact that, lacking interventional data, the observed dependence between S and G is due to a causal connection or is spurious

(apparent dependence arising from a common cause, R). (see Simpson's paradox)

To determine whether a causal relation is identified from an arbitrary Bayesian network with unobserved variables, one can use the three rules of 'do-calculus'^[1][4] and test whether all do terms can be removed from the expression of that relation, thus confirming that the desired quantity is estimable from frequency data.^[5]

Using a Bayesian network can save considerable amounts of memory over exhaustive probability tables, if the dependencies in the joint distribution are sparse. For example, a naive way of storing the conditional probabilities of 10 two-valued variables as a table requires storage space for ${\displaystyle 2^{10}=1024}$ values. If no variable's local distribution depends on more than three parent variables, the Bayesian network representation stores at most ${\displaystyle 10\cdot 2^3=80}$ values.

One advantage of Bayesian networks is that it is intuitively easier for a human to understand (a sparse set of) direct dependencies and local distributions than complete joint distributions.

Inference and learning[edit]

Bayesian networks perform three main inference tasks:

Inferring unobserved variables[edit]

Because a Bayesian network is a complete model for its variables and their relationships, it can be used to answer probabilistic queries about them. For example, the network can be used to update knowledge of the state of a subset of variables when other variables (the evidence variables) are observed. This process of computing the posterior distribution of variables given evidence is called probabilistic inference. The posterior gives a universal sufficient statistic for detection applications, when choosing values for the variable subset that minimize some expected loss function, for instance the probability of decision error. A Bayesian network can thus be considered a mechanism for automatically applying Bayes' theorem to complex problems.

The most common exact inference methods are: variable elimination, which eliminates (by integration or summation) the non-observed non-query variables one by one by distributing the sum over the product; clique tree propagation, which caches the computation so that many variables can be queried at one time and new evidence can be propagated quickly; and recursive conditioning and AND/OR search, which allow for a space–time tradeoff and match the efficiency of variable elimination when enough space is used. All of these methods have complexity that is exponential in the network's treewidth. The most common approximate inference algorithms are importance sampling, stochastic MCMC simulation, mini-bucket elimination, loopy belief propagation, generalized belief propagation and variational methods.

Parameter learning[edit]

In order to fully specify the Bayesian network and thus fully represent the joint probability distribution, it is necessary to specify for each node X the probability distribution for X conditional upon X's parents. The distribution of X conditional upon its parents may have any form. It is common to work with discrete or Gaussian distributions since that simplifies calculations. Sometimes only constraints on a distribution are known; one can then use the principle of maximum entropy to determine a single distribution, the one with the greatest entropy given the constraints. (Analogously, in the specific context of a dynamic Bayesian network, the conditional distribution for the hidden state's temporal evolution is commonly specified to maximize the entropy rate of the implied stochastic process.)

Often these conditional distributions include parameters that are unknown and must be estimated from data, e.g., via the maximum likelihood approach. Direct maximization of the likelihood (or of the posterior probability) is often complex given unobserved variables. A classical approach to this problem is the expectation-maximization algorithm, which alternates computing expected values of the unobserved variables conditional on observed data, with maximizing the complete likelihood (or posterior) assuming that previously computed expected values are correct. Under mild regularity conditions this process converges on maximum likelihood (or maximum posterior) values for parameters.

A more fully Bayesian approach to parameters is to treat them as additional unobserved variables and to compute a full posterior distribution over all nodes conditional upon observed data, then to integrate out the parameters. This approach can be expensive and lead to large dimension models, making classical parameter-setting approaches more tractable.

Structure learning[edit]

In the simplest case, a Bayesian network is specified by an expert and is then used to perform inference. In other applications the task of defining the network is too complex for humans. In this case the network structure and the parameters of the local distributions must be learned from data.

Automatically learning the graph structure of a Bayesian network (BN) is a challenge pursued within machine learning. The basic idea goes back to a recovery algorithm developed by Rebane and Pearl^[6] and rests on the distinction between the three possible patterns allowed in a 3-node DAG:

Junction patterns

Pattern	Model
Chain	${\displaystyle X\to Y\to Z}$
Fork	${\displaystyle X\leftarrow Y\to Z}$
Collider	${\displaystyle X\to Y\leftarrow Z}$

The first 2 represent the same dependencies (${\displaystyle X}$ and ${\displaystyle Z}$ are independent given ${\displaystyle Y}$) and are, therefore, indistinguishable. The collider, however, can be uniquely identified, since ${\displaystyle X}$ and ${\displaystyle Z}$ are marginally independent and all other pairs are dependent. Thus, while the skeletons (the graphs stripped of arrows) of these three triplets are identical, the directionality of the arrows is partially identifiable. The same distinction applies when ${\displaystyle X}$ and ${\displaystyle Z}$ have common parents, except that one must first condition on those parents. Algorithms have been developed to systematically determine the skeleton of the underlying graph and, then, orient all arrows whose directionality is dictated by the conditional independences observed.^[1][7][8][9]

An alternative method of structural learning uses optimization-based search. It requires a scoring function and a search strategy. A common scoring function is posterior probability of the structure given the training data, like the BIC or the BDeu. The time requirement of an exhaustive search returning a structure that maximizes the score is superexponential in the number of variables. A local search strategy makes incremental changes aimed at improving the score of the structure. A global search algorithm like Markov chain Monte Carlo can avoid getting trapped in local minima. Friedman et al.^[10][11] discuss using mutual information between variables and finding a structure that maximizes this. They do this by restricting the parent candidate set to k nodes and exhaustively searching therein.

A particularly fast method for exact BN learning is to cast the problem as an optimization problem, and solve it using integer programming. Acyclicity constraints are added to the integer program (IP) during solving in the form of cutting planes.^[12] Such method can handle problems with up to 100 variables.

In order to deal with problems with thousands of variables, a different approach is necessary. One is to first sample one ordering, and then find the optimal BN structure with respect to that ordering. This implies working on the search space of the possible orderings, which is convenient as it is smaller than the space of network structures. Multiple orderings are then sampled and evaluated. This method has been proven to be the best available in literature when the number of variables is huge.^[13]

Another method consists of focusing on the sub-class of decomposable models, for which the MLE have a closed form. It is then possible to discover a consistent structure for hundreds of variables.^[14]

Learning Bayesian networks with bounded treewidth is necessary to allow exact, tractable inference, since the worst-case inference complexity is exponential in the treewidth k (under the exponential time hypothesis). Yet, as a global property of the graph, it considerably increases the difficulty of the learning process. In this context it is possible to use K-tree for effective learning.^[15]

Statistical introduction[edit]

Given data ${\displaystyle x}$ and parameter ${\displaystyle \theta }$, a simple Bayesian analysis starts with a prior probability (prior) ${\displaystyle p(\theta )}$ and likelihood${\displaystyle p(x\mid \theta )}$ to compute a posterior probability${\displaystyle p(\theta \mid x)\propto p(x\mid \theta )p(\theta )}$.

Often the prior on ${\displaystyle \theta }$ depends in turn on other parameters ${\displaystyle \phi }$ that are not mentioned in the likelihood. So, the prior ${\displaystyle p(\theta )}$ must be replaced by a likelihood ${\displaystyle p(\theta \mid \phi )}$, and a prior ${\displaystyle p(\phi )}$ on the newly introduced parameters ${\displaystyle \phi }$ is required, resulting in a posterior probability

${\displaystyle p(\theta ,\phi x)\propto p(x\theta )p(\theta \phi )p(\phi ).}$

This is the simplest example of a hierarchical Bayes model.^{[clarification needed]}

The process may be repeated; for example, the parameters ${\displaystyle \phi }$ may depend in turn on additional parameters ${\displaystyle \psi }$, which require their own prior. Eventually the process must terminate, with priors that do not depend on unmentioned parameters.

Introductory examples[edit]

Given the measured quantities ${\displaystyle x_1,\dots ,x_n}$each with normally distributed errors of known standard deviation${\displaystyle \sigma }$,

${\displaystyle x_i\sim N({\theta }_i,{\sigma }^2)}$

Suppose we are interested in estimating the ${\displaystyle {\theta }_i}$. An approach would be to estimate the ${\displaystyle {\theta }_i}$ using a maximum likelihood approach; since the observations are independent, the likelihood factorizes and the maximum likelihood estimate is simply

${\displaystyle {\theta }_i=x_i}$.

However, if the quantities are related, so that for example the individual ${\displaystyle {\theta }_i}$have themselves been drawn from an underlying distribution, then this relationship destroys the independence and suggests a more complex model, e.g.,

${\displaystyle x_i\sim N({\theta }_i,{\sigma }^2),}$

${\displaystyle {\theta }_i\sim N(\phi ,{\tau }^2)}$,

Bayesian Network Definition

with improper priors${\displaystyle \phi \sim }$flat, ${\displaystyle \tau \sim }$flat${\displaystyle \in (0,\mathrm{\infty })}$. When ${\displaystyle n\ge 3}$, this is an identified model (i.e. there exists a unique solution for the model's parameters), and the posterior distributions of the individual ${\displaystyle {\theta }_i}$ will tend to move, or shrink away from the maximum likelihood estimates towards their common mean. This shrinkage is a typical behavior in hierarchical Bayes models.

Restrictions on priors[edit]

Some care is needed when choosing priors in a hierarchical model, particularly on scale variables at higher levels of the hierarchy such as the variable ${\displaystyle \tau }$ in the example. The usual priors such as the Jeffreys prior often do not work, because the posterior distribution will not be normalizable and estimates made by minimizing the expected loss will be inadmissible.

Definitions and concepts[edit]

Several equivalent definitions of a Bayesian network have been offered. For the following, let G = (V,E) be a directed acyclic graph (DAG) and let X = (X_v), v ∈ V be a set of random variables indexed by V.

Factorization definition[edit]

X is a Bayesian network with respect to G if its joint probability density function (with respect to a product measure) can be written as a product of the individual density functions, conditional on their parent variables:^[16]

${\displaystyle p(x)=\prod _{v\in V}p\left(x_v{x}_{\mathrm{pa}(v)}\right)}$

where pa(v) is the set of parents of v (i.e. those vertices pointing directly to v via a single edge).

For any set of random variables, the probability of any member of a joint distribution can be calculated from conditional probabilities using the chain rule (given a topological ordering of X) as follows:^[16]

${\displaystyle \mathrm{P}(X_1=x_1,\dots ,X_n=x_n)=\prod _{v=1}^n\mathrm{P}\left(X_v=x_v\mid X_{v+1}=x_{v+1},\dots ,X_n=x_n\right)}$

Using the definition above, this can be written as:

${\displaystyle \mathrm{P}(X_1=x_1,\dots ,X_n=x_n)=\prod _{v=1}^n\mathrm{P}(X_v=x_v\mid X_j=x_j}$ for each ${\displaystyle X_j}$ which is a parent of ${\displaystyle X_v)}$

The difference between the two expressions is the conditional independence of the variables from any of their non-descendants, given the values of their parent variables.

Local Markov property[edit]

X is a Bayesian network with respect to G if it satisfies the local Markov property: each variable is conditionally independent of its non-descendants given its parent variables:^[17]

${\displaystyle X_v\perp \perp X_{V\setminus \mathrm{de}(v)}\mid X_{\mathrm{pa}(v)}\text{for all}v\in V}$

where de(v) is the set of descendants and V de(v) is the set of non-descendants of v.

This can be expressed in terms similar to the first definition, as

${\displaystyle \mathrm{P}(X_v=x_v\mid X_i=x_i}$ for each ${\displaystyle X_i}$ which is not a descendant of ${\displaystyle X_v)=P(X_v=x_v\mid X_j=x_j}$ for each ${\displaystyle X_j}$ which is a parent of ${\displaystyle X_v)}$

The set of parents is a subset of the set of non-descendants because the graph is acyclic.

Developing Bayesian networks[edit]

Developing a Bayesian network often begins with creating a DAG G such that X satisfies the local Markov property with respect to G. Sometimes this is a causal DAG. The conditional probability distributions of each variable given its parents in G are assessed. In many cases, in particular in the case where the variables are discrete, if the joint distribution of X is the product of these conditional distributions, then X is a Bayesian network with respect to G.^[18]

Markov blanket[edit]

The Markov blanket of a node is the set of nodes consisting of its parents, its children, and any other parents of its children. The Markov blanket renders the node independent of the rest of the network; the joint distribution of the variables in the Markov blanket of a node is sufficient knowledge for calculating the distribution of the node. X is a Bayesian network with respect to G if every node is conditionally independent of all other nodes in the network, given its Markov blanket.^[17]

d-separation[edit]

This definition can be made more general by defining the 'd'-separation of two nodes, where d stands for directional.^[19][20] Let P be a trail from node u to v. A trail is a loop-free, undirected (i.e. all edge directions are ignored) path between two nodes. Then P is said to be d-separated by a set of nodes Z if any of the following conditions holds:

Dynamic Bayesian Networks Python

• P contains (but does not need to be entirely) a directed chain, ${\displaystyle u\dots \leftarrow m\leftarrow \dots v}$ or ${\displaystyle u\dots \to m\to \dots v}$, such that the middle node m is in Z,
• P contains a fork, ${\displaystyle u\dots \leftarrow m\to \dots v}$, such that the middle node m is in Z, or
• P contains an inverted fork (or collider), ${\displaystyle u\dots \to m\leftarrow \dots v}$, such that the middle node m is not in Z and no descendant of m is in Z.

The nodes u and v are d-separated by Z if all trails between them are d-separated. If u and v are not d-separated, they are d-connected.

X is a Bayesian network with respect to G if, for any two nodes u, v:

${\displaystyle X_u\perp \perp X_v\mid X_Z}$

where Z is a set which d-separates u and v. (The Markov blanket is the minimal set of nodes which d-separates node v from all other nodes.)

Causal networks[edit]

Although Bayesian networks are often used to represent causal relationships, this need not be the case: a directed edge from u to v does not require that X_v be causally dependent on X_u. This is demonstrated by the fact that Bayesian networks on the graphs:

${\displaystyle a\to b\to c\text{and}a\leftarrow b\leftarrow c}$

are equivalent: that is they impose exactly the same conditional independence requirements.

A causal network is a Bayesian network with the requirement that the relationships be causal. The additional semantics of causal networks specify that if a node X is actively caused to be in a given state x (an action written as do(X = x)), then the probability density function changes to that of the network obtained by cutting the links from the parents of X to X, and setting X to the caused value x.^[1] Using these semantics, the impact of external interventions from data obtained prior to intervention can be predicted.

Inference complexity and approximation algorithms[edit]

In 1990, while working at Stanford University on large bioinformatic applications, Cooper proved that exact inference in Bayesian networks is NP-hard.^[21] This result prompted research on approximation algorithms with the aim of developing a tractable approximation to probabilistic inference. In 1993, Dagum and Luby proved two surprising results on the complexity of approximation of probabilistic inference in Bayesian networks.^[22] First, they proved that no tractable deterministic algorithm can approximate probabilistic inference to within an absolute errorɛ< 1/2. Second, they proved that no tractable randomized algorithm can approximate probabilistic inference to within an absolute error ɛ < 1/2 with confidence probability greater than 1/2.

At about the same time, Roth proved that exact inference in Bayesian networks is in fact #P-complete (and thus as hard as counting the number of satisfying assignments of a conjunctive normal form formula (CNF) and that approximate inference within a factor 2^n1-ɛ for every ɛ > 0, even for Bayesian networks with restricted architecture, is NP-hard.^[23][24]

In practical terms, these complexity results suggested that while Bayesian networks were rich representations for AI and machine learning applications, their use in large real-world applications would need to be tempered by either topological structural constraints, such as naïve Bayes networks, or by restrictions on the conditional probabilities. The bounded variance algorithm^[25] was the first provable fast approximation algorithm to efficiently approximate probabilistic inference in Bayesian networks with guarantees on the error approximation. This powerful algorithm required the minor restriction on the conditional probabilities of the Bayesian network to be bounded away from zero and one by 1/p(n) where p(n) was any polynomial on the number of nodes in the network n.

Software[edit]

Notable software for Bayesian networks include:

• Just another Gibbs sampler (JAGS) - Open-source alternative to WinBUGS. Uses Gibbs sampling.
• OpenBUGS - Open-source development of WinBUGS.
• SPSS Modeler - Commercial software that includes an implementation for Bayesian networks.
• Stan (software) - Stan is an open-source package for obtaining Bayesian inference using the No-U-Turn sampler, a variant of Hamiltonian Monte Carlo.
• WinBUGS - One of the first computational implementations of MCMC samplers. No longer maintained.

History[edit]

The term Bayesian network was coined by Judea Pearl in 1985 to emphasize:^[26]

• the often subjective nature of the input information
• the reliance on Bayes' conditioning as the basis for updating information
• the distinction between causal and evidential modes of reasoning^[27]

In the late 1980s Pearl's Probabilistic Reasoning in Intelligent Systems^[28] and Neapolitan's Probabilistic Reasoning in Expert Systems^[29] summarized their properties and established them as a field of study.

See also[edit]

• Dempster–Shafer theory – a Generalization of Bayes' theorem

Notes[edit]

1. ^ ^abcdPearl, Judea (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press. ISBN978-0-521-77362-1. OCLC42291253.
2. ^'The Back-Door Criterion'(PDF). Retrieved 2014-09-18.
3. ^'d-Separation without Tears'(PDF). Retrieved 2014-09-18.
4. ^Pearl J (1994). 'A Probabilistic Calculus of Actions'. In Lopez de Mantaras R, Poole D (eds.). UAI'94 Proceedings of the Tenth international conference on Uncertainty in artificial intelligence. San Mateo CA: Morgan Kaufmann. pp. 454–462. arXiv:1302.6835. Bibcode:2013arXiv1302.6835P. ISBN1-55860-332-8.
5. ^Shpitser I, Pearl J (2006). 'Identification of Conditional Interventional Distributions'. In Dechter R, Richardson TS (eds.). Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence. Corvallis, OR: AUAI Press. pp. 437–444. arXiv:1206.6876.
6. ^Rebane G, Pearl J (1987). 'The Recovery of Causal Poly-trees from Statistical Data'. Proceedings, 3rd Workshop on Uncertainty in AI. Seattle, WA. pp. 222–228. arXiv:1304.2736.
7. ^Spirtes P, Glymour C (1991). 'An algorithm for fast recovery of sparse causal graphs'(PDF). Social Science Computer Review. 9 (1): 62–72. doi:10.1177/089443939100900106.
8. ^Spirtes P, Glymour CN, Scheines R (1993). Causation, Prediction, and Search (1st ed.). Springer-Verlag. ISBN978-0-387-97979-3.
9. ^Verma T, Pearl J (1991). 'Equivalence and synthesis of causal models'. In Bonissone P, Henrion M, Kanal LN, Lemmer JF (eds.). UAI '90 Proceedings of the Sixth Annual Conference on Uncertainty in Artificial Intelligence. Elsevier. pp. 255–270. ISBN0-444-89264-8.
10. ^Friedman N, Geiger D, Goldszmidt M (November 1997). 'Bayesian Network Classifiers'. Machine Learning. 29 (2–3): 131–163. doi:10.1023/A:1007465528199.
11. ^Friedman N, Linial M, Nachman I, Pe'er D (August 2000). 'Using Bayesian networks to analyze expression data'. Journal of Computational Biology. 7 (3–4): 601–20. CiteSeerX10.1.1.191.139. doi:10.1089/106652700750050961. PMID11108481.
12. ^Cussens J (2011). 'Bayesian network learning with cutting planes'(PDF). Proceedings of the 27th Conference Annual Conference on Uncertainty in Artificial Intelligence: 153–160.
13. ^Scanagatta M, de Campos CP, Corani G, Zaffalon M (2015). 'Learning Bayesian Networks with Thousands of Variables'. NIPS-15: Advances in Neural Information Processing Systems. 28. pp. 1855–1863.
14. ^Petitjean F, Webb GI, Nicholson AE (2013). Scaling log-linear analysis to high-dimensional data(PDF). International Conference on Data Mining. Dallas, TX, USA: IEEE.
15. ^M. Scanagatta, G. Corani, C. P. de Campos, and M. Zaffalon. Learning Treewidth-Bounded Bayesian Networks with Thousands of Variables. In NIPS-16: Advances in Neural Information Processing Systems 29, 2016.
16. ^ ^abRussell & Norvig 2003, p. 496.
17. ^ ^abRussell & Norvig 2003, p. 499.
18. ^Neapolitan RE (2004). Learning Bayesian networks. Prentice Hall. ISBN978-0-13-012534-7.
19. ^Geiger D, Verma T, Pearl J (1990). 'Identifying independence in Bayesian Networks'(PDF). Networks. 20: 507–534. doi:10.1177/089443939100900106.
20. ^Richard Scheines, D-separation
21. ^Cooper GF (1990). 'The Computational Complexity of Probabilistic Inference Using Bayesian Belief Networks'(PDF). Artificial Intelligence. 42 (2–3): 393–405. doi:10.1016/0004-3702(90)90060-d.
22. ^Dagum P, Luby M (1993). 'Approximating probabilistic inference in Bayesian belief networks is NP-hard'. Artificial Intelligence. 60 (1): 141–153. CiteSeerX10.1.1.333.1586. doi:10.1016/0004-3702(93)90036-b.
23. ^D. Roth, On the hardness of approximate reasoning, IJCAI (1993)
24. ^D. Roth, On the hardness of approximate reasoning, Artificial Intelligence (1996)
25. ^Dagum P, Luby M (1997). 'An optimal approximation algorithm for Bayesian inference'. Artificial Intelligence. 93 (1–2): 1–27. doi:10.1016/s0004-3702(97)00013-1.
26. ^Pearl J (1985). Bayesian Networks: A Model of Self-Activated Memory for Evidential Reasoning(UCLA Technical Report CSD-850017). Proceedings of the 7th Conference of the Cognitive Science Society, University of California, Irvine, CA. pp. 329–334. Retrieved 2009-05-01.
27. ^Bayes T, Price (1763). 'An Essay towards solving a Problem in the Doctrine of Chances'. Philosophical Transactions of the Royal Society. 53: 370–418. doi:10.1098/rstl.1763.0053.
28. ^Pearl J (1988-09-15). Probabilistic Reasoning in Intelligent Systems. San Francisco CA: Morgan Kaufmann. p. 1988. ISBN978-1558604797.
29. ^Neapolitan RE (1989). Probabilistic reasoning in expert systems: theory and algorithms. Wiley. ISBN978-0-471-61840-9.

References[edit]

• Ben Gal I (2007). 'Bayesian Networks'(PDF). In Ruggeri F, Kennett RS, Faltin FW (eds.). Encyclopedia of Statistics in Quality and Reliability. John Wiley & Sons. doi:10.1002/9780470061572.eqr089. ISBN978-0-470-01861-3.
• Bertsch McGrayne S. The Theory That Would not Die. New Haven: Yale University Press.
• Borgelt C, Kruse R (March 2002). Graphical Models: Methods for Data Analysis and Mining. Chichester, UK: Wiley. ISBN978-0-470-84337-6.
• Borsuk ME (2008). 'Ecological informatics: Bayesian networks'. In Jørgensen, Sven Erik, Fath, Brian (eds.). Encyclopedia of Ecology. Elsevier. ISBN978-0-444-52033-3.
• Castillo E, Gutiérrez JM, Hadi AS (1997). 'Learning Bayesian Networks'. Expert Systems and Probabilistic Network Models. Monographs in computer science. New York: Springer-Verlag. pp. 481–528. ISBN978-0-387-94858-4.
• Comley JW, Dowe DL (June 2003). 'General Bayesian networks and asymmetric languages'. Proceedings of the 2nd Hawaii International Conference on Statistics and Related Fields.
• Comley JW, Dowe DL (2005). 'Minimum Message Length and Generalized Bayesian Nets with Asymmetric Languages'. In Grünwald PD, Myung IJ, Pitt MA (eds.). Advances in Minimum Description Length: Theory and Applications. Neural information processing series. Cambridge, Massachusetts: Bradford Books (MIT Press) (published April 2005). pp. 265–294. ISBN978-0-262-07262-5. (This paper puts decision trees in internal nodes of Bayes networks using Minimum Message Length (MML).
• Darwiche A (2009). Modeling and Reasoning with Bayesian Networks. Cambridge University Press. ISBN978-0521884389.
• Dowe, David L. (2011-05-31). 'Hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness'(PDF). Philosophy of Statistics. Elsevier. pp. 901–982. ISBN9780080930961.
• Fenton N, Neil ME (November 2007). 'Managing Risk in the Modern World: Applications of Bayesian Networks'(PDF). A Knowledge Transfer Report from the London Mathematical Society and the Knowledge Transfer Network for Industrial Mathematics. London (England): London Mathematical Society.
• Fenton N, Neil ME (July 23, 2004). 'Combining evidence in risk analysis using Bayesian Networks'(PDF). Safety Critical Systems Club Newsletter. 13 (4). Newcastle upon Tyne, England. pp. 8–13. Archived from the original(PDF) on 2007-09-27.
• Gelman A, Carlin JB, Stern HS, Rubin DB (2003). 'Part II: Fundamentals of Bayesian Data Analysis: Ch.5 Hierarchical models'. Bayesian Data Analysis. CRC Press. pp. 120–. ISBN978-1-58488-388-3.
• Heckerman, David (March 1, 1995). 'Tutorial on Learning with Bayesian Networks'. In Jordan, Michael Irwin (ed.). Learning in Graphical Models. Adaptive Computation and Machine Learning. Cambridge, Massachusetts: MIT Press (published 1998). pp. 301–354. ISBN978-0-262-60032-3.

Also appears as Heckerman, David (March 1997). 'Bayesian Networks for Data Mining'. Data Mining and Knowledge Discovery. 1 (1): 79–119. doi:10.1023/A:1009730122752.

An earlier version appears as Technical Report MSR-TR-95-06, Microsoft Research, March 1, 1995. The paper is about both parameter and structure learning in Bayesian networks.

• Jensen FV, Nielsen TD (June 6, 2007). Bayesian Networks and Decision Graphs. Information Science and Statistics series (2nd ed.). New York: Springer-Verlag. ISBN978-0-387-68281-5.
• Karimi K, Hamilton HJ (2000). 'Finding temporal relations: Causal bayesian networks vs. C4. 5'(PDF). Twelfth International Symposium on Methodologies for Intelligent Systems.
• Korb KB, Nicholson AE (December 2010). Bayesian Artificial Intelligence. CRC Computer Science & Data Analysis (2nd ed.). Chapman & Hall (CRC Press). doi:10.1007/s10044-004-0214-5. ISBN978-1-58488-387-6.
• Lunn D, Spiegelhalter D, Thomas A, Best N (November 2009). 'The BUGS project: Evolution, critique and future directions'. Statistics in Medicine. 28 (25): 3049–67. doi:10.1002/sim.3680. PMID19630097.
• Neil M, Fenton N, Tailor M (August 2005). Greenberg, Michael R. (ed.). 'Using Bayesian networks to model expected and unexpected operational losses'(PDF). Risk Analysis. 25 (4): 963–72. doi:10.1111/j.1539-6924.2005.00641.x. PMID16268944.
• Pearl J (September 1986). 'Fusion, propagation, and structuring in belief networks'. Artificial Intelligence. 29 (3): 241–288. doi:10.1016/0004-3702(86)90072-X.
• Pearl J (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Representation and Reasoning Series (2nd printing ed.). San Francisco, California: Morgan Kaufmann. ISBN978-0-934613-73-6.
• Pearl J, Russell S (November 2002). 'Bayesian Networks'. In Arbib MA (ed.). Handbook of Brain Theory and Neural Networks. Cambridge, Massachusetts: Bradford Books (MIT Press). pp. 157–160. ISBN978-0-262-01197-6.
• Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, ISBN0-13-790395-2.
• Zhang NL, Poole D (May 1994). 'A simple approach to Bayesian network computations'(PDF). Proceedings of the Tenth Biennial Canadian Artificial Intelligence Conference (AI-94).: 171–178. This paper presents variable elimination for belief networks.

Further reading[edit]

• Conrady S, Jouffe L (2015-07-01). Bayesian Networks and BayesiaLab - A practical introduction for researchers. Franklin, Tennessee: Bayesian USA. ISBN978-0-9965333-0-0.
• Charniak E (Winter 1991). 'Bayesian networks without tears'(PDF). AI Magazine.
• Kruse R, Borgelt C, Klawonn F, Moewes C, Steinbrecher M, Held P (2013). Computational Intelligence A Methodological Introduction. London: Springer-Verlag. ISBN978-1-4471-5012-1.
• Borgelt C, Steinbrecher M, Kruse R (2009). Graphical Models - Representations for Learning, Reasoning and Data Mining (Second ed.). Chichester: Wiley. ISBN978-0-470-74956-2.

External links[edit]

• A hierarchical Bayes Model for handling sample heterogeneity in classification problems, provides a classification model taking into consideration the uncertainty associated with measuring replicate samples.
• Hierarchical Naive Bayes Model for handling sample uncertainty, shows how to perform classification and learning with continuous and discrete variables with replicated measurements.